DC power

The power is a direct current (DC) circuit is equal to the voltage multiplied by the current. The power can also be calculated with the resistance using Ohm's law.

Formulas

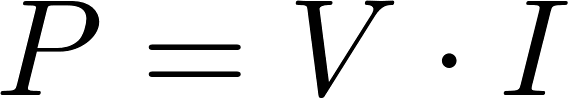
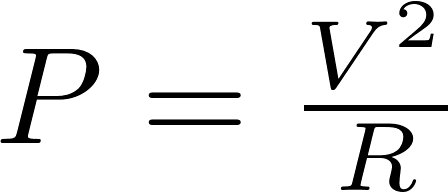
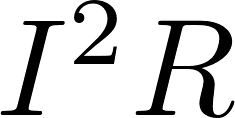
P is the symbol for power and is measured in watt (W).
V is the symbol for voltage and is measured in volt (V).
I is the symbol for current and is measured in ampere (A).
R is the symbol for resistance and is measured in ohm (Ω).

Calculator

Enter two values to calculate the remaining two.