Zener diode

A zener diode also allows the current to flow in the opposite direction when the zener voltage is reached instead of exclusively letting current flow from the anode to the cathode. Zener diodes are used to supply reference voltages and to prevent overvoltage.

Formulas

The following formulas can be used to calculate the resistance, the power of the resistor and the power of the zener diode.

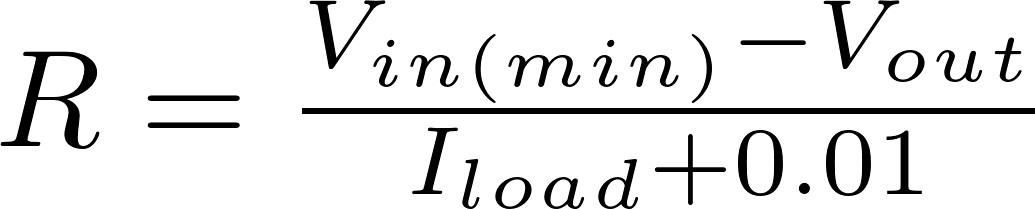
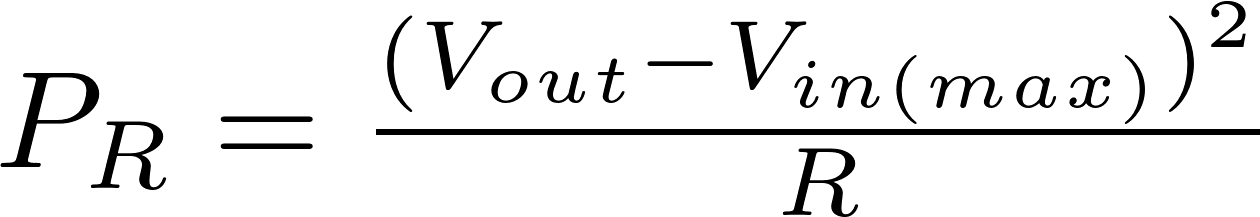
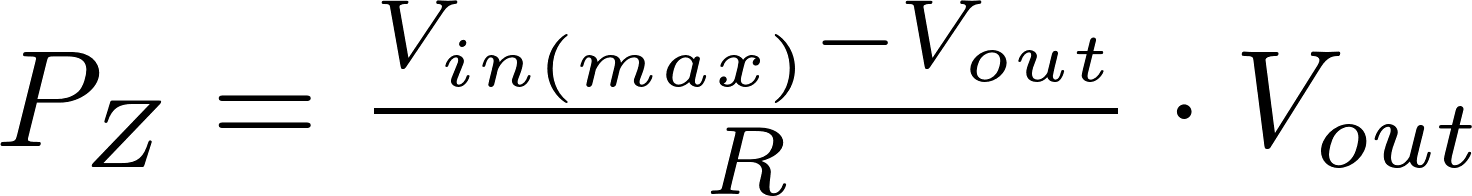
R is the symbol for resistance and is measured in ohm (Ω).
V _in is the input voltage and is measured in volt (V)
V _out is the output voltage and is measured in volt (V)
P is the symbol for power and is measured in watt (W).

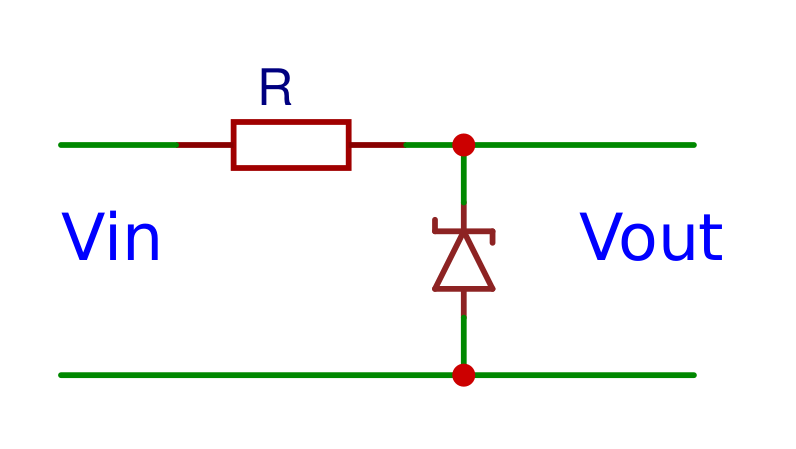
Calculator

You can use this calculator to calculate the power of the zener and the resistance and power of the resistor.